리뷰 날짜: 2024.02.05
2021
Félix Raimundo, Laetitia Meng-Papaxanthos, Céline Vallot, Jean-Philippe Vert
https://www.sciencedirect.com/science/article/abs/pii/S2452310021000172
Preliminary
Gaussian noise
- 정규분포를 가지는 noise
- 일반적인 noise로 어느 정도 랜덤하며 자연계에서 쉽게 볼 수 있다.
Overdispersion
- the observation that variation is higher than would be expected
- Overdispersion is often mentioned together with zero-inflation, but it is distinct: Overdispersion also includes the case where none of your data points are actually ‘zero’.
Zero-inflation
- distribution that allows for
frequent zero-valued observations

ZinbWave
- Zero-Inflated Negative Binomial Model for RNA-Seq data
- a general and flexible model for the analysis of high-dimensional zero-inflated count data, such as those recorded in single-cell RNA-seq assays.
- Implements a general and flexible zero-inflated negative binomial model that can be used to provide a low-dimensional representations of single-cell RNA-seq data. The model accounts for zero inflation (dropouts), over-dispersion, and the count nature of the data. The model also accounts for the difference in library sizes and optionally for batch effects and/or other covariates, avoiding the need for pre-normalize the data.
- https://bioconductor.org/packages/devel/bioc/vignettes/zinbwave/inst/doc/intro.html
An introduction to ZINB-WaVE
Pollen, Alex A, Tomasz J Nowakowski, Joe Shuga, Xiaohui Wang, Anne A Leyrat, Jan H Lui, Nianzhen Li, et al. 2014. “Low-coverage single-cell mRNA sequencing reveals cellular heterogeneity and activated signaling pathways in developing cerebral cortex.”
bioconductor.org
Bayesian model
- 불확실성을 확률로 나타내고, 사전 정보를 사용하여 사후 확률을 갱신하는 방식으로 데이터를 분석한다.
- Bayes’ Theorem을 이용한다: P(A∣B)=P(B)P(B∣A)⋅P(A)
AE (Autoencoder)
- 입력이 들어왔을 때, 해당 입력 데이터를 최대한 압축시킨 후 , 데이터의 특징을 추출하여 다시 본래의 입력 형태로 복원시키는 신경망
- 데이터를 압축하는 부분을 Encoder, 복원하는 부분을 Decoder라고 하며 압축과정에서 추출한 의미 있는 데이터 Z를 보통 latent vector라고 부르며 이를 latent variable, feature 과도 같이 부른다
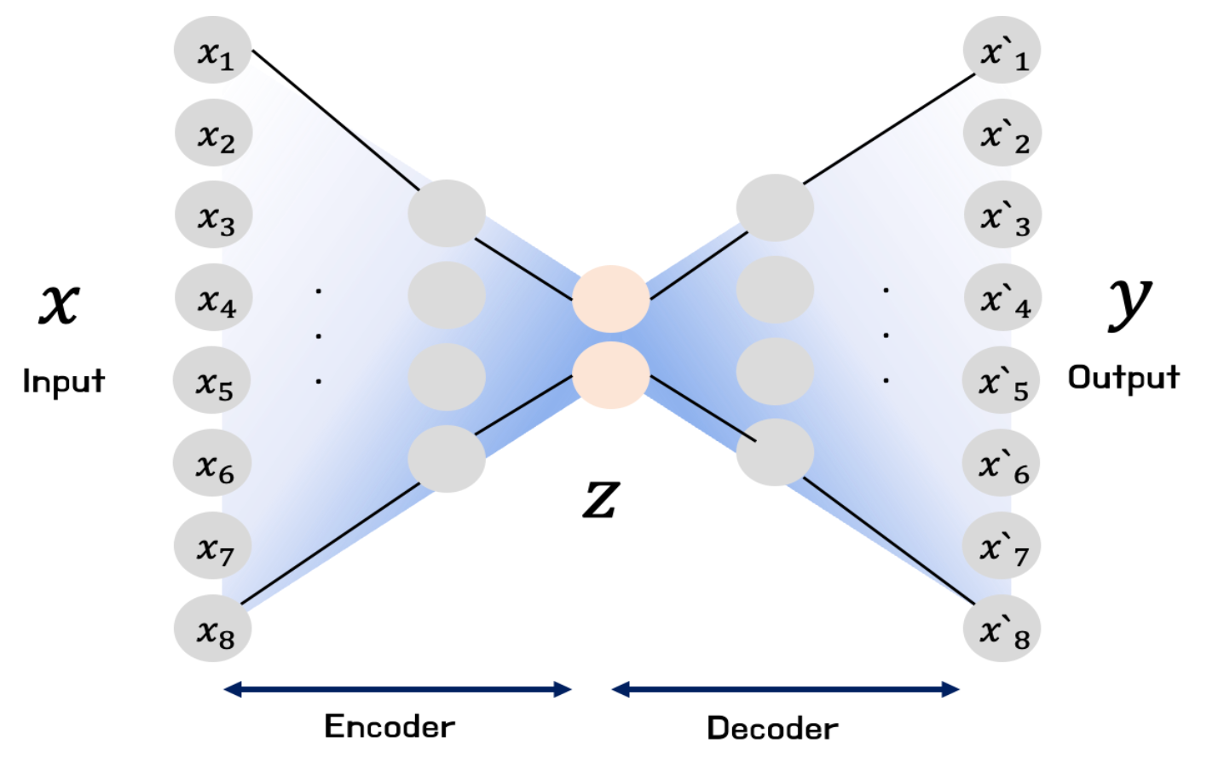
(V)AE: (Variational) Autoencoder
- Input image X를 잘 설명하는 feature를 추출하여 Latent vector z 에 담고, Latent vector z를 통해 X와 유사하지만 새로운 데이터를 생성하는 것을 목표로 한다. 이때, 각 feature는 Gaussian distribution을 따른다고 가정하고 mean과 variation을 나타내어 준다.
- VAE는 probabilistic autoencoder이다. 따라서 training이 끝난 이후에도 output이 부분적으로 우연에 의해 결정된다.
- VAE는 generative autoencoder이므로,training datset에서 sampling된 것과 같은 새로운 sample을 생성할 수 있다.
- VAE는 generative model이므로, decoder를 학습시키는 것을 주 목적으로 한다
- VAE 의 encoder는 주어진 입력에 대하여 mean and standard deviation coding을 만든다
- 실제 코딩은 Gaussian distribution으로부터 randomly sampled 되며, 이렇게 sampling된 코딩을 decoder의 input으로 사용해 원본 입력으로 재구성하게 된다

t-SNE (t-distributed Stochastic Neighbor Embedding)
- high-dimensional vector의 visualization을 위한 방법
- 고차원의 벡터로 표현되는 데이터 간의 neighbor structure를 보존하는 2차원의 embedding vector를 학습함으로써, 고차원의 데이터를 2차원 지도로 표현한다
→ 고차원 공간에서 유사한 두 벡터가 2차원 공간에서도 유사하도록 원 공간에서의 점들 간 유사도를 보존하면서 차원을 축소한다
- 벡터 시각화를 위한 다른 알고리즘들보다 안정적인 임베딩 학습 결과를 보여준다
→ t-SNE가 데이터 간 거리를 stochastic probability로 변환하여 임베딩에 이용하기 때문
- stochastic probability는 perplexity에 의해 조절된다
PCA
- 차원 축소에 쓰이는 기법으로, 모든 특성을 살릴 수 없더라도 최대한 특징을 살리며 차원을 낮춰준다.
- eigenvector, eigenvalue: Ax = λx를 만족하는 nonzero vector x가 eigenvector이다.
- 또한, Ax = λx에서 x가 nontrivial solution이 존재할 때 scalar λ가 eigenvalue가 된다.
- 여기서 x를 λ에 상응하는 eigenvector이라고 한다.
- PC (principal component): 분산이 최대로 보존 될 수 있도록 하는, 데이터를 정사영시킬 새로운 축
- 분산의 최대값을 찾는 이유: 정보 손실을 최소화 하기 위함
- PC를 찾기 위해서는 covariance matrix(공분산 행렬) 의 eigen vector를 찾아야 하고, 이 값 중 가장 큰 값이 우리가 원하는 PC 에 만족한다고 볼 수 있으며 이를 PCA의 원리로 볼 수 있다.
matrix factorization
- a class of collaborative filtering models
- the model factorizes the user-item interaction matrix (e.g., rating matrix) into the product of two lower-rank matrices, capturing the low-rank structure of the user-item interactions

Latent Dirichlet allocation (LDA)
- **토픽 모델링: 문서의 집합에서 토픽을 찾아내는 프로세스
- LDA는 토픽 모델링의 대표적인 알고리즘
- 문서들은 토픽들의 혼합으로 구성되어 있으며, 토픽들은 확률 분포에 기반하여 단어들을 생성한다고 가정한다
- 데이터가 주어지면, LDA는 문서가 생성된 과정을 역추적(역공학, reverse engineering)한다
- 토픽의 개수를 의미하는 변수를 hyperparameter k로 두고, k를 지정한다
- reference: https://lettier.com/projects/lda-topic-modeling/
Latent Dirichlet Allocation Topic Modeling by David Lettier
lettier.com
non-negative matrix factorization (NMF)
- 음수를 포함하지 않는 행렬 X를 음수를 포함하지 않는 행렬 W와 H의 곱으로 분해하는 알고리즘; X = WH
- H의 각 행은 하나의 feature가 되고, W의 한 행은 각각의 feature를 얼마만큼 섞어 쓸 것인지에 관한 weight의 의미를 갖게 된다

- 추출하게 되는 feature들이 모두 non-negative feature이기 때문에 유용하다
- 그러나 많은 경우에 사용되는 matrix factorization 방법이나 차원 감소 방법에서는 획득할 수 없는 feature들이 음수이면 안된다는 제한사항 같은 것이 없기 때문에, 데이터의 특성인 non-negativity를 보존할 수 있다는 보장을 받을 수 없다는 한계가 있다
- PCA나 SVD와 같은 factorization 방법에 비해 데이터의 구조를 조금 더 잘 반영할 수 있어서, feature들의 독립성을 잘 파악할 수 있다
Introduction
- Cells are the fundamental units of organisms, exhibiting heterogeneity in various biological functions.
- e.g., There is heterogeneity between cells in the lung cancer tissue.


- Traditional research focuses on population-level averages, neglecting individual cell characteristics.
- It ignores the differences in gene expression regulation between different population and single cells. Single-cell
sequencing, which is sequenced at the individual cell level, solves the heterogeneity of genetic variation between different cells.

Omics
- 생물학 데이터의 대량 생산을 목적으로 하는 많은 실험 기법들의 통칭
Single-cell Omics
- With single-cell omics technologies getting widespread adoption, computational methods are urgently needed to process the large amounts of data they produce.
- therefore, seen by many as a promising way to infer biological knowledge and develop predictive models from single-cell omics data, which provide a high-dimensional characterization of large quantities of cells.
- the development of ML approaches to analyze single-cell omics data has been a very active field of research recently.
transcriptomic
mRNA, rRNA, tRNA 및 기타 non-coding RNA를 포함한 모든 RNA 분자 세트는 하나 또는 세포 집단에서 생성되고, 전사체학은 이러한 RNA 구조 및 기능을 연구하는 학문
epigenomic
- 단백질 및 RNA 결합제, 대체 DNA 구조 및 DNA에 대한 화학적 변형을 포함한 genome의 지원 구조. 세포핵내의 히스톤 단백질과 관계된 메틸레이션과 아세틸레이션 등의 유전체 수정(modification)을 연구하는 학문
- 현대 기술에는 Hi-C에 의한 염색체 구조화, 다양한 ChIP-seq 및 proteomic fractionation과 결합한 기타 시퀀싱 방법, bisulfite 시퀀싱과 같은 cytosines의 화학적 변형을 찾는 시퀀싱 방법이 포함
Multimodal
시각, 청각을 비롯한 여러 인터페이스를 통해서 정보를 주고받는 것을 말하는 개념
- multimodal AI: 다양한 채널의 모달리티를 동시에 받아들여서 학습하고 사고하는 AI
→ 인간이 사물을 받아들이는 다양한 방식과 동일하게 학습하는 AI
trajectory inference
a computational technique used in single-cell transcriptomics to determine the pattern of a dynamic process experienced by cells and then arrange cells based on their progression through the process
From raw data to useful representations
- Raw single-cell transcriptomic count data, as well as their epigenomic counterparts, provide a high-dimensional and noisy description of each cell by assessing the activity of thousands of genes or DNA loci simultaneously.
- Transforming raw count data to a lower-dimensional representation of each cell using the dimension reduction (DR) technique is a useful step to remove technical noise and prepare data for visualization, classification or further analysis tasks.

- Traditional methods like scran and Seurat v2 utilize standard Principal Component Analysis (PCA) on log-transformed count data for Dimensionality Reduction (DR) in single-cell RNA sequencing (scRNA-seq).
- However, recent advancements in DR for scRNA-seq data introduce novel models departing from the Gaussian noise assumption of PCA.
- These newer models explicitly consider statistical properties of raw count data, addressing challenges such as overdispersion and dropout-induced zero-inflation.
- Notable examples include the matrix factorization-based model ZinbWave, nonparametric Bayesian models, (Variational) Autoencoders ((V)AE).
- (V)AEs learn a low-dimensional representation of input data (cell transcriptomes) capable of reconstructing the original data.
- Several (V)AE models tailored for scRNA-seq data, such as scVI, DCA, SAVER, and scVAE, have been proposed.
- Notably, some methods leverage hyperbolic geometry for DR.
- While these models differ in specific assumptions, such as count data statistical models or prior distribution of low-dimensional representations, they share a common architecture.
- An intriguing characteristic of these models is their computational scalability, often implemented using deep learning libraries designed for efficiently handling millions or more input points.
- But finding the optimal dimensionality reduction (DR) approach for single-cell RNA sequencing (scRNA-seq) data is complex.
- Deep learning-based (V)AE face challenges, requiring a large number of cells and sensitivity to parameter choices.
- Simpler models remain competitive, especially with datasets containing only a few hundred or thousand cells. Training complex machine learning models, like (V)AE or t-distributed stochastic neighbor embedding (tSNE), poses practical difficulties, emphasizing the importance of reproducibility and avoiding overfitting to specific experiments.
- Recent DR methods for single-cell epigenomic data include those based on standard PCA models, matrix factorization with latent Dirichlet allocation, and VAE. Preprocessing, particularly how reads are binned into regions of interest, is crucial for the success of these methods.
- A noteworthy idea for small datasets is leveraging larger annotated datasets to learn embeddings using transfer learning or domain adaptation techniques. Embeddings learned by PCA, non-negative matrix factorization (NMF), or (denoising) AEs on one dataset have proven useful for clustering and surface protein prediction on other datasets.
- However, these methods have a limitation: embeddings are learned on one dataset and applied to another without simultaneous analysis, limiting the ability to train models on multiple datasets.
- After DR, standard clustering algorithms identify cell types, with sensitivity to hyperparameter choices. Differential expression tools identify marker genes once cells are clustered. Matching cells to known types involves querying reference databases using tools like Cell BLAST, scMap, scQuery, or CellFishing.jl.
- However, these methods can be sensitive to batch effects.
Reference
[유전학 중요개념 정리] 오믹스 (Omics) 와 단일 세포 시퀀싱 (Single cell sequencing)
현재 있는 미국의 연구실은 다양한 Omics 데이터를 종합적으로 분석하여, 소아 신증후군의 정밀 의료 실현을 위한 연구를 진행하고 있습니다. 아래의 관련 포스팅과 같이, 다양한 유전체 연구 결
2wordspm.wordpress.com
https://www.frontiersin.org/journals/genetics/articles/10.3389/fgene.2022.1100016/full
Frontiers | Single-cell omics: A new direction for functional genetic research in human diseases and animal models
Over the past decade, with the development of high-throughput single-cell sequencing technology, single-cell omics has been emerged as a powerful tool to und...
www.frontiersin.org
https://www.samsungsds.com/kr/insights/multi-modal-ai.html
인간처럼 사고하는 멀티모달(Multi Modal) AI란? | 인사이트리포트 | 삼성SDS
AI는 어떻게 사물의 개념을 받아들일까요? AI는 명령어만으로는 그 단어가 어떤 형태로 세상에 존재하는지 이해하지 못해요! 그래서 AI가 인간처럼 인식할 수 있도록 만들어진 것이 '멀티모달 AI'
www.samsungsds.com
https://velog.io/@swan9405/PCA
머신러닝 - PCA (Principal Component Analysis)
1. PCA(Principal Component Analysis) - 주성분 분석이란? 주성분이란 전체 데이터(독립변수들)의 분산을 가장 잘 설명하는 성분을 말한다. 변수의 개수 = 차원의 개수 e.g.) iris 데이터에서, 4개의 독립변인
velog.io
https://biometry.github.io/APES//LectureNotes/2016-JAGS/Overdispersion/OverdispersionJAGS.html
Introduction: what is overdispersion?
Introduction: what is overdispersion? Overdispersion describes the observation that variation is higher than would be expected. Some distributions do not have a parameter to fit variability of the observation. For example, the normal distribution does that
biometry.github.io
[연구 일지] 2. Zero-Inflated Poisson Regression
https://www.otago.ac.nz/__data/assets/pdf_file/0031/284890/zero-inflated-models-301201.pdf
https://d2l.ai/chapter_recommender-systems/mf.html
21.3. Matrix Factorization — Dive into Deep Learning 1.0.3 documentation
d2l.ai
[딥러닝] AutoEncoder 개념 및 종류
Autoencoder(오토인코더)란 representation learning 작업에 신경망을 활용하도록 하는 비지도 학습 방법 입력이 들어왔을 때, 해당 입력 데이터를 최대한 압축시킨 후 , 데이터의 특징을 추출하여 다시 본
velog.io
https://deepinsight.tistory.com/126
[정리노트] [AutoEncoder의 모든것] Chap3. AutoEncoder란 무엇인가(feat. 자세히 알아보자)
AutoEncoder의 모든 것 본 포스팅은 이활석님의 'AutoEncoder의 모든 것'에 대한 강연 자료를 바탕으로 학습을 하며 정리한 문서입니다. 이활석님의 동의를 받아 출처를 밝히며 강의 자료의 일부를 인
deepinsight.tistory.com
https://lovit.github.io/nlp/representation/2018/09/28/tsne/
t-Stochastic Neighbor Embedding (t-SNE) 와 perplexity
t-Stochastic Nearest Neighbor (t-SNE) 는 vector visualization 을 위하여 자주 이용되는 알고리즘입니다. t-SNE 는 고차원의 벡터로 표현되는 데이터 간의 neighbor structure 를 보존하는 2 차원의 embedding vector 를 학
lovit.github.io
https://iamseungjun.tistory.com/18
UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction
UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction UMAP은 주어진 manifold가 uniform 하다는 가정 하에 차원 축소의 관점에서 manifold learning을 수행할 수 있다. Data manifold를 UMAP으로 해석하기 전
iamseungjun.tistory.com
https://nate9389.tistory.com/2203
【알고리즘】 7-2강. UMAP(uniform manifold approximation and projection)
7-2강. UMAP(uniform manifold approximation and projection) 추천글 : 【알고리즘】 7강. 차원 축소 알고리즘 1. 개요 [본문]2. 1단계. k-simplex 정의 [본문]3. 2단계. k-simplex 정의 최적화 [본문]4. 3단계. g
nate9389.tistory.com